2015年陕西数学理科试题及答案word在线版
2015年陕西理科数学选择题
1.设集合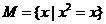 ,
,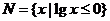 ,则
,则
A.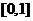 B.
B. C.
C.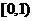 D.
D.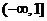
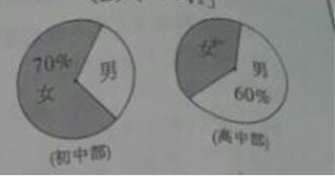
2.某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为
A.167 B.137 C.123 D.93
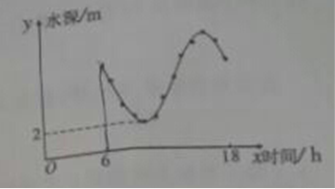
3.如图,某港口一天6时到18时的水深变化曲线近似满足函数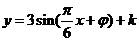 ,据此函数可知,这段时间水深(单位:m)的最大值为
,据此函数可知,这段时间水深(单位:m)的最大值为
A.5 B.6 C.8 D.10
4.二项式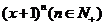 的展开式中
的展开式中 的系数为15,则
的系数为15,则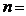
A.4 B.5 C.6 D.7
5.一个几何体的三视图如图所示,则该几何体的表面积为
A.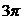 B.
B. C.
C.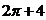 D.
D.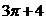
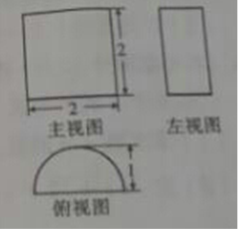
6.“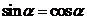 ”是“
”是“ ”的
”的
A充分不必要条件B必要不充分条件C充分必要条件D既不充分也不必要
7.对任意向量 ,下列关系式中u恒成立的是
,下列关系式中u恒成立的是
A. B.
B.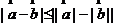 C.
C.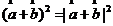 D.
D.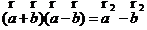
8.根据右边的图,当输入x为2005时,输出的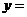
A28 B10 C4 D2
9.设 ,若
,若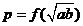 ,
,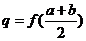 ,
, ,则下列关系式中正确的是
,则下列关系式中正确的是
A. B.
B. C.
C. D.
D.
10.某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额表所示,如果生产1吨甲乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为
A.12万元 B.16万元 C.17万元 D.18万元
11.设复数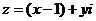
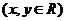 ,若
,若 ,则
,则 的概率
的概率
A.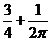 B.
B.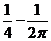 C.
C.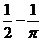 D.
D.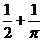
12.对二次函数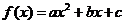 (a为非零常数),四位同学分别给出下列结论,其中有且仅有一个结论是错误的,则错误的结论是
(a为非零常数),四位同学分别给出下列结论,其中有且仅有一个结论是错误的,则错误的结论是
A.-1是 的零点 B.1是
的零点 B.1是 的极值点 C.3是
的极值点 C.3是 的极值 D.点
的极值 D.点 在曲线
在曲线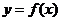 上
上
2015年陕西理科数学填空
13.中位数1010的一组数构成等差数列,其末项为2015,则该数列的首项为
14.若抛物线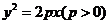 的准线经过双曲线
的准线经过双曲线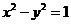 的一个焦点,则p=
的一个焦点,则p=
15.设曲线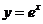 在点(0,1)处的切线与曲线
在点(0,1)处的切线与曲线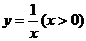 上点p处的切线垂直,则p的坐标为
上点p处的切线垂直,则p的坐标为
16.如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线表示),则原始的最大流量与当前最大流量的比值为

2015年陕西理科数学解答题
(本大题共6小题,共70分.解答须写出文字说明、证明过程和演算步骤.)
17、(本小题满分12分)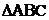 的内角
的内角 ,
,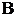 ,
,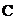 所对的边分别为
所对的边分别为 ,
,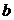 ,
,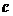 .向量
.向量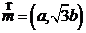 与
与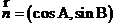 平行.
平行.
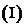 求
求 ;
;
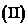 若
若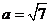 ,
, 求
求 的面积.
的面积.
18、(本小题满分12分)如图 ,在直角梯形
,在直角梯形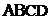 中,
中,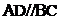 ,
, ,
,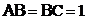 ,
,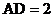 ,
, 是
是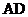 的中点,
的中点,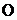 是
是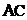 与
与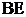 的交点.将
的交点.将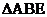 沿
沿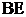 折起到
折起到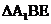 的位置,如图
的位置,如图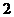 .
.
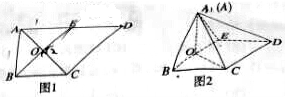
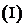 证明:
证明: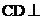 平面
平面 ;
;
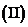 若平面
若平面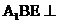 平面
平面 ,求平面
,求平面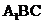 与平面
与平面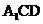 夹角的余弦值.
夹角的余弦值.
19、(本小题满分12分)设某校新、老校区之间开车单程所需时间为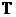 ,
, 只与道路畅通状况有关,对其容量为
只与道路畅通状况有关,对其容量为 的样本进行统计,结果如下:
的样本进行统计,结果如下:
 (分钟) (分钟) | 25 | 30 | 35 | 40 |
| 频数(次) | 20 | 30 | 40 | 10 |
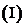 求
求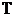 的分布列与数学期望
的分布列与数学期望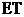 ;
;
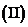 刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
 20、(本小题满分12分)已知椭圆
20、(本小题满分12分)已知椭圆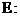
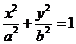 (
(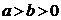 )的半焦距为
)的半焦距为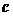 ,原点
,原点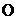 到经过两点
到经过两点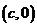 ,
,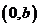 的直线的距离为
的直线的距离为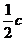 .
.
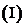 求椭圆
求椭圆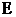 的离心率;
的离心率;
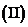 如图,
如图,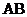 是圆
是圆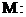
 的一条直径,若椭圆
的一条直径,若椭圆 经过
经过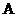 ,
,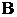 两点,求椭圆
两点,求椭圆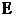 的方程.
的方程.
(文章来源招生考试网,转载请注明原文出处: https://www.sczsxx.com/html/gaokaoziyuan/liniangaokaoshiti/2015/0609/119524.html)
- 热门内容



